The Origin of Gravity in the new Vacuum Paradigm
Min Tae Kim, kimnogravity@gmail.com
Affiliations: The KMT Institute for Theory of Everything, Daejeon, Republic of Korea.
In modern physics, gravity is still an unknown physical phenomenon. We sought to find its origin from a new concept of vacuum: The vacuum is composed of a very dense solid medium with a regular matrix, where matter is vibration energy added to the vacuum matrix. This vibration radiates “matter wave” to distort the vacuum matrix locally as much as the energy. Three-dimensional symmetry of distortion develops around the stationary matter. Any inertial movement is interpreted as the movement of the vibration site, through which the symmetry of distortion is broken. This process yields a gradient of the distortion in the direction of movement, which in turn sustains the inertial movement so that the kinetic energy is preserved. When the movement is rotational, a gradient of the distortion is also generated across the rotation orbit, attracting nearby particles on to the plane of rotation. If the movement is spherically symmetric, like the random vibration of a lattice point, this attraction is also spherically symmetric. This is the origin of gravity, and mass is a collective energy of the vibrating sites gathered due to gravity in the vacuum matrix.
1. Introduction
Gravity is one of the essential parts of Newtonian dynamics and also of the general theory of relativity (GR theory). Gravity is known as one kind of force of nature. But its origin is still mysterious for which only a few hypothetical theories exist.1,2 One of these theories is called entropic gravity in that gravity is regarded as a phenomenon caused by quantum entanglement of small bits of spacetime information.1 Entropic gravity is sustained, as entropy is increasing with time according to the 2nd law of thermodynamics. This theory is not yet proven and still in a lot of controversies.3 Gravity is also approached combined with quantum mechanics. In this quantum theory of gravity, gravitons are introduced to mediate the gravitational field in the quantum field.2 However, gravity is nonrenormalizable, so that the theory is limited for any meaningful predictions.4
Up to now, the GR theory appears to be the one that best describes gravity. This theory has been tested and proven in many ways: it has predicted the precession of the perihelion of Mercury, light deflection by the Sun, gravitational redshift, etc.5 The theory also predicts gravitational waves that carry away energy as gravitational radiation.6,7 Recently the first observation was made as the gravitational waves radiated from a pair of merging black holes.8,9
Here we are thinking about how gravitational waves can move through empty spaces and how can light waves travel in the vacuum where nothing exists. This paper considers the possible existence of a vacuum medium which carries the gravitational and electromagnetic waves. Thereafter, the inertial movement of a particle is characterized under the premise that the vacuum is composed of a very dense and cold medium with very little or no energy available and a very regular matrix. Gravity is inferred from the characteristics of the inertial movement to give the origin of gravity in the solid vacuum matrix. Matter waves from the vibration of the vacuum matrix are also related to the inertial and gravitational movement, for which mass is shown to be another expression for the vibration energy stored in the solid vacuum matrix.
2. A new paradigm for the vacuum
Light propagation in the solid vacuum medium
There were severe debates about the nature of light in the Newtonian era. Newton was an advocate of the particle nature of light,10 and light had been considered to be a collection of particles until the wave characteristics of light were experimentally proven.11 If light is a wave, a medium to carry the wave was needed. So an imaginary fluid called “ether” was hypothesized. But the existence of this hypothetical “fluid” was disproved by Michelson and Molly,12 and light has been accepted to propagate in the vacuum without any medium. However, if we think that a shear wave can only propagate in solid media, and light is a shear wave, it can be imagined that light propagates through the solid medium as a wave. In fact, there are theories that the density of vacuum is enormously high,13,14 around 1096 kg/m3, the Planck density, incomparable to the total observable mass of the universe of 1053 kg.15 A similar concept of vacuum was proposed by Paul Dirac in 1930, in that the vacuum consists of the infinite sea (Dirac sea) of particles with negative energy.16 This model predicted the presence of positrons and was discovered by Anderson in 1932.17
If light is a kind of wave and propagates in the solid vacuum medium, we may find its similarity with the propagation of sound waves (elastic waves) in solid. Sound waves are classified into pressure waves and shear waves. Generally, pressure waves are faster than shear waves.18 As light is a shear wave, we consider only shear sound waves, the speed of which is given by 19
𝑣𝑠=√(𝐺𝑠/𝜌) (1),
Here Gs is the shear modulus of the solid. We note the similarity of E = mc2, Einstein's energy-mass equivalence, to the speed of the shear wave in solid in Eq. (1). Dividing both sides of the equivalence equation by volume, the speed of light c is written as
𝑐=√(𝐺𝑉/𝜌𝑉) (2).
Here, GV = E/V (the energy density) and m/V = ρV (the mass density of the vacuum). Eq. (2) has the same form as Eq. (1). GV in Eq. (2) may be regarded as the shear modulus of the solid vacuum. Using the Plank density 5.16x1094 g/cm3 for ρV, we have GV to be ca. 4.64x10100 GPa, which we may call the Plank shear modulus. As the speed of sound waves in a solid is lower when the thermodynamic energy of the solid is higher, namely at higher temperatures and pressures,20-22 the speed of light is lower in ordinary matters than in the solid vacuum. The refractive index is thus always more than 1 for all the materials.23 Ordinary matters have more energy than the solid vacuum. So they are hotter and thus less stiff for the propagation of light waves.

Figure 1. A swan moves on the water to make asymmetric waves. By Dick Daniels (http://theworldbirds.org/)
Conservation of energy in the inertial frame (in the solid vacuum)
Here we will newly interpret the inertial movement of a particle in the solid vacuum matrix to associate it with gravity. When a swan moves at a constant velocity over the surface of the water, its movement will form a concentric wave that continuously spreads in all directions, as shown in Fig. 1. The wavelength becomes shorter in the forward direction and longer in the backward direction due to the forward movement of the swan. Similarly, we consider that a particle moves through the solid vacuum at a constant velocity. This particle will move without changing the velocity and direction unless external forces are applied. This is the law of inertia, Newton's first law of motion. Unlike the movement of a swan on the surface of the water, energy is not consumed for the movement in the inertial frame. A moving particle has two masses, the rest mass and the mass in the moving defined in terms of Einstein's special relativity, the relativistic mass. The total energy of a moving particle expressed by the mass-energy equivalence is higher than that of a stationary one. In our new vacuum paradigm, the energy of a moving particle is the energy of distortion of the solid vacuum induced by the movement of the particle. When a particle travels at a constant velocity, the solid vacuum is compressed in the forward direction and relaxed in the opposite direction. Besides, the solid vacuum will also be distorted normal to the direction of travel. This is the Doppler effect, as shown in Fig. 2. The kinetic energy due to the movement is then the energy of distortion of the solid vacuum. Inversely we can say that a particle moves when there is a difference in the distortion of the solid vacuum. It moves from the less distorted side toward the more distorted side. When the distortion in the forward direction increases, the particle will accelerate in that direction.

Figure 2. An image showing the Doppler’s effect. By Pbroks13 (https://commons.wikimedia.org/w/index.php?curid=5029074)
What should be the energy of distortion Ed stored in the solid vacuum due to an inertial movement? It is deduced from the difference in the energy of the relativistic mass m and the rest mass m0, as
𝐸𝑑=(𝑚−𝑚0)𝑐2=(𝛾−1)𝑚0𝑐2 (3)
Here, γ is called the Lorentz factor, a measure of the increased mass due to the movement at the velocity v:
γ=1/√(1+𝑣/𝑐)√(1−𝑣/𝑐)=1/𝑧 (4)
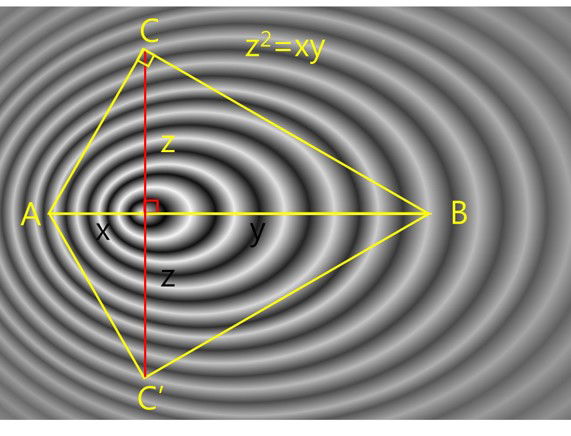
In the regime of v << c, the distortion energy is approximated to Ed = ½mv2, being the kinetic energy of the classical mechanics. γ can be regarded as a parameter designating the degree of distortion of the solid vacuum associated with the movement. In Eq. (4) z, the reciprocal of γ, is the geometric mean of 1+v/c and 1-v/c, as conceptually shown the using two symmetric right triangles in Fig. 3 in which x = 1-v/c and y = 1+v/c, respectively. x+y = 2 and z2 = xy. Regarding +v/c as the compressed distortion in the forward direction or -v/c the stretched distortion in the backward direction, the kinetic energy is asymmetric distortion energy stored in the solid vacuum.
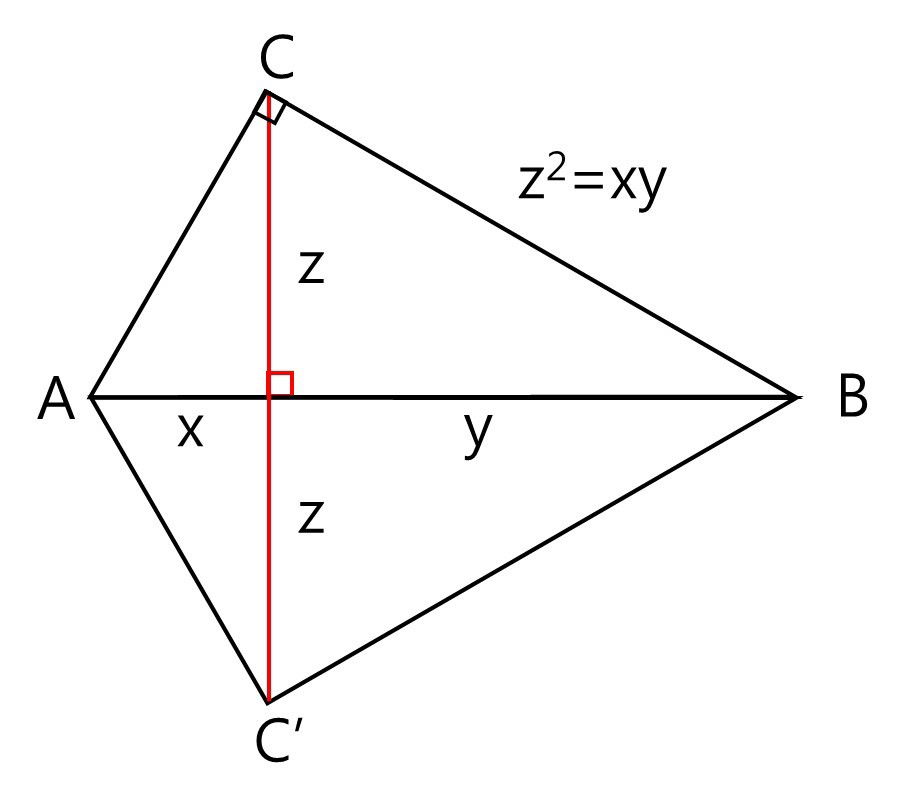
Figure 3. Geometric presentation for the meaning of z, the reciprocal of γ. x and y represent 1-v/c and 1+v/c, respectively. x+y = 2 is constant and z2 = xy.
3. Origin of gravity in the solid vacuum
Interpretation of gravity in the new vacuum paradigm
As mass is another expression of energy through mass-energy equivalence, this energy should be stored in the solid vacuum, as with the kinetic energy. As mentioned in the previous section, the kinetic energy is the energy of asymmetric distortion of the solid vacuum due to the movement of a particle. When a spherical particle is stationary in the solid vacuum, the distortion will be point symmetric for which the center of symmetry is at the center of mass of the particle. If the distortion of the solid vacuum is only originated from the movement, then the stationary mass-energy of a particle means back-and-forth movements (oscillation or vibration) in a random mode around a point. So the distortion is balanced in all directions. The distortion of the solid vacuum shall be intense near the particle and become weaker on going away from the center of mass, as the gravitational field does.
We now consider two spherical particles, one with mass m1 and one with m2 separated by a distance r in space, as shown in Fig. 4. There will be a difference in the intensity of distortion of the solid vacuum in the regions between the particles and the outside of them. The distortion at the point P will be more intense than at Q because P is nearer to m1 than Q when the distance from P to the center of m2 is the same as that from Q to the center. The distortion is asymmetric regarding the particle m2. The particle m2 will approach m1, as with the movement in the inertial frame. As m2 moves toward m1, the intensity of distortion between the two particles increases. The approach velocity further increases. The particle feels an acceleration force. This is the origin of gravity in the solid vacuum. The distortion of the solid vacuum is the source of mass-energy and is also the source of gravity. So, the gravitational mass and inertial mass are inevitably the same.
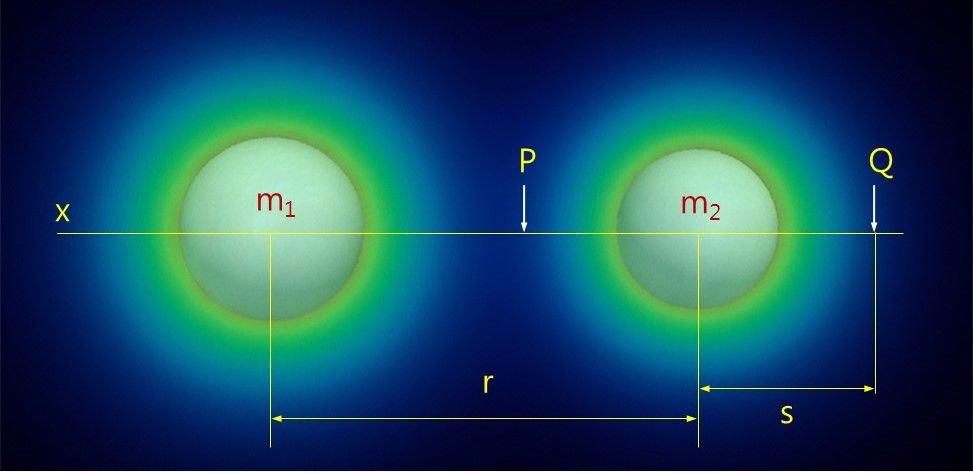
Figure 4. Two spherical particles m1 and m2 in the solid vacuum separated by a distance r. The distance of P and Q from the center of m2 is the same. The distortion at P is more intense than at Q due to the difference in the distance from the center of m1.
A particle moving at a constant velocity v stores energy in the solid vacuum as in Eq. (4). Let γ-1 in in Eq. (3) to be the increased distortion Δδ of the solid vacuum due to the movement in the inertial frame, namely γ-1 = Δδ. v may be written as a function of Δδ from the relation γ-1= Δδ as:
𝑣=𝑐√(2Δδ +Δδ2)/(Δδ+1 ) (5)
Normally v << c and thus Δδ ~ 0, so that Eq. (5) is approximated to
𝑣=𝑐√(2𝛥δ) (6)
As shown in Fig. 2, which shows the Doppler effect, the solid vacuum is also distorted in the normal direction to the direction of movement. However, since the distortion in the normal direction is symmetric about the line of traveling of the particle, it does not affect its movement. If the hypotenuse of the right triangle (AB) in Fig. 3 is the direction of travel (to the left), the distortions in the upper and lower directions normal to this side are each γ = z-1 = Δδ+1. These cancel each other to 0 to yield the maximum velocity in the direction of travel. If we consider the distortion γ = Δδ +1 of the upper of the upper direction only, we have the (imaginary) normal velocity vn from Eq. (4) as
𝑣𝑛 = c√Δδ/(Δδ+1) (7)
For v << c, or Δδ ~ 0, Eq. (7) is approximated to
𝑣𝑛 = c√Δδ (8)
Comparing Eq. (6) and (8), we see that the ratio v/vn is √2 for any directions on the plane normal to the movement. We may say that the balanced distortion of Δδ on this plane has led to the maximum gradient distortion of 2Δδ to the direction of the movement.to the direction of the movement. However, if a particle makes a rotational movement instead of a linear one, the distortion of the solid vacuum in the normal direction (radial direction of the rotation) will not cancel each other. The balance will then be destroyed. Particles on the plane of the rotational orbit will feel an increasing gradient in the distortion toward the center of rotation, and the particles outside of the orbit will be attracted to the rotating particle. It means an attractive force can be generated by the rotational movement of a massive body in our new vacuum paradigm.
Movement of a particle in the distortional field of the solid vacuum
Now suppose a planet that revolves around the Sun at the orbital radius of rO. The mass of the Sun is M and of the planet is mp. When this planet revolves steadily, the energy due to the distortion of the solid vacuum surrounding the Sun (potential energy) and that due to the imaginary outward radial velocity vR should be the same. That is
(𝛾−1)𝑚𝑝𝑐2=𝐺𝑀𝑚𝑝/𝑟 (9).
The radial velocity vR is then from the definition of 𝛾 in Eq. (4)
𝑣𝑅=𝑐√[𝑟𝑆(4𝑟+𝑟𝑆)]/(2𝑟+𝑟𝑆) (10).
Here rS = 2GM/c2, called the Schwarzschild radius. rS of the Sun is around 2.95 km, too much smaller than the radius of the Sun, 696,392 km,24 so that vR is approximated to
𝑣𝑅=𝑐√𝑟𝑆/𝑟=√(2𝐺𝑀)/𝑟 (11).
Here, G is the gravitational constant. Comparing Eq. (6) and Eq. (11), 2Δδ generated from the movement in the radial direction should balance the distortion due to the presence of mass M, and it is rS/rO at the orbital radius of rO. How can we obtain such a distortion as if there were a movement in the radial direction? It is actually originated from the orbital movement of the planet. As mentioned in the previous section, a rotational movement of a particle induces a gradient in the distortion of the solid vacuum normal to the tangent of the rotational movement. The distortion generated by the orbital velocity vO for a given orbital radius of rO should then compensate for the distortion of the solid vacuum rS/rO in the radial direction due to the presence of mass M. We see from Eq. (6) and (8) that the distortion in the circumferential direction will be rS/2rO when the radial velocity is given as Eq. (11). The circumferential velocity (orbital velocity, vO) will be then 1/√2 times the radial velocity, that is
𝑣𝑂=𝑐√𝑟𝑆/2𝑟𝑂 (12).
If the eccentricity is not large, the orbit is close to a circle. The average velocity vO of the orbit can be approximated by the orbital period T and the semi-major axis ra as follows:
𝑣𝑂=2𝜋𝑟𝑎/𝑇=√(𝐺𝑀)/𝑟𝑎 (13).
The term on the right-hand side is obtained from Kepler's third law. Eq. (12) and (13) are fully consistent if the orbit radius is the semi-major axis. The observed orbital velocity and calculated values of the planets of the solar system from Eq. (12) are compared in Fig. 5. We see that the orbital velocity estimated from our new vacuum paradigm well coincides with the observed and that Kepler's third law can be understood in our new vacuum paradigm.

Figure 5. Comparison of the observed orbital velocity and calculated values of the solar system from Eq. (12).
The acceleration aR in the radial direction is obtained by differentiating the equation (11) as follows:
𝑎𝑅=𝑑𝑣𝑅/𝑑𝑡=(𝑑𝑟/𝑑𝑡)(𝑑𝑣𝑅/𝑑𝑟)=−𝑐2𝑟𝑆/2𝑟2=−𝐺𝑀/𝑟2 (14)
Acceleration is opposite to the direction of outward radial movement. This is the law of gravity. According to our new paradigm of vacuum, G can be regarded as an index of the mechanical properties of the solid vacuum. Our new solid vacuum model and the inference regarding the origin of gravity are further verified through the calculation of the deflection of light by the Sun and the precession of Mercury. Details are shown in the Appendices, [A1] for the light deflection, and [A2] for the precession.
4. Matter wave in the solid vacuum
In this study, we showed that the asymmetric distortion of the solid vacuum is the origin of movements in the inertial frame. The asymmetry is sustained as long as a particle moves. This is the law of inertia in the Newtonian dynamics. The kinetic energy of a moving particle is stored as an energy of this asymmetric distortion in the solid vacuum. The relativistic mass is then the rest mass plus the energy of the asymmetric distortion. If a particle moves randomly in a spherically symmetric way, namely, it vibrates around a point in a three-dimensional random mode, the distortion of the solid vacuum will be developed in a spherically symmetric way around the particle. The rest mass of a particle is then understood to be the energy of distortion of the solid vacuum stored due to its three-dimensional random vibration. The inertial mass and the gravitational mass are inevitably the same in the new vacuum paradigm. Thus we do not have to insist on the equivalence principle on which the GR theory relies.
If mass is the vibrational energy of the solid vacuum (lattice point), matter will be the source of wave generated from the vibration and propagate through the solid vacuum. We may call it matter wave. In modern physics, there is the concept of matter wave proposed by de Broglie in response to the duality of light (wave + particle).25 The de Broglie wavelength λ has the following relationship with the momentum p of a moving particle.26
λ=ℎ/𝑝=ℎ/𝑚𝑣 (15)
Here, h is the Planck constant. This hypothesis was validated in polyatomic molecules such as fullerene (C60)27 as well as electrons 28,29 and atoms,30 and thus matter is accepted to have the duality of particle and wave. Quantum mechanics interprets this wave as a function of probability finding a particle for a given time and space.31 How can we interpret this matter wave in terms of our new vacuum paradigm? According to Eq. (15), the inverse of the wavelength, the wave number, is proportional to the mass and velocity. We understand the distortion of the solid vacuum is more intense near a more massive particle moving at a higher velocity than a less massive one moving at a lower velocity. The wave number can be regarded as an index for the intensity of the distortion of the solid vacuum around a moving particle. A moving particle with the velocity v is then steadily generating a matter wave with the wavelength given in Eq. (15) and the frequency fm from its vibration given as 32
𝑓𝑚=𝑚c2/ℎ=𝛾𝑚0c2/ℎ=𝛾𝑓𝑚0 (16).
Eq. (16) is the Plank-Einstein relation for matter wave. We apparently see from Eq. (16) that the vibration of the solid vacuum matrix is the origin of mass (m) and energy (mc2). In terms of the Doppler effect,33 the frequency of a matter wave in the forward direction 𝑓𝑚+ and the backward direction 𝑓𝑚− will be respectively
𝑓𝑚+=𝑓𝑚0/(1−𝑣/𝑐) ; 𝑓𝑚−=𝑓𝑚0/(1+𝑣/𝑐) (17).
Hence, the frequency of matter wave of a moving particle is the geometric mean of the forward and backward frequency of matter wave:
𝑓𝑚=√(𝑓𝑚+𝑓𝑚-)=γ𝑓𝑚0 (18).
As 𝑓𝑚−𝑓𝑚0=(𝛾−1)𝑓𝑚0 from Eq. (16), we see that the asymmetric distortion of the solid vacuum has been increased due to an increase in the frequency of matter wave of a moving particle. The increased distortion of the solid vacuum of a moving particle Δ𝛿 corresponds to
Δ𝛿=𝛾−1= (𝑓𝑚−𝑓𝑚0)/𝑓𝑚0 (19),
which is the rate of change in the frequency of matter wave due to the movement.
5. Summary - The solid vacuum as the platform for mass and wave
We have defined the vacuum as a solid medium without energy or with very low energy. The propagation of light could then be easily understood in the new vacuum paradigm, as similarly as that of sound waves in solids. The energy-mass equivalence is nothing but an equation describing the speed of the propagation of light waves in the solid vacuum.Matter is also a kind of wave, and mass is another expression of the frequency of matter wave as apparently shown in Eq. (16). In this context, we may say that the solid vacuum provides a platform for mass and wave. This platform has a three-dimensional matrix, like a solid crystal with lattice. The symmetric vibration of a lattice point in the solid vacuum yields a particle with mass corresponding to the frequency of the vibration in Eq. (16). This vibration propagates radially outward into the whole solid vacuum matrix to build up a spherically symmetric distortion in the solid vacuum around the particle. When this symmetric distortion is broken, the vibration site moves to the neighboring site in the direction of increasing distortion. This process is accompanied by the change in the frequency of vibration in Eq. (18), as well as the change in the mass in Eq. (16) equivalently. The inertial movement of the vibration site preserves the distortion difference in the solid vacuum, and thus the kinetic energy is preserved. When a particle is near to a massive body, the particle feels asymmetric distortion along the direction of the center of the massive body due to the symmetric distortion of the solid vacuum generated by the vibration of the body. The particle will then move toward the body, which leads again to the increase in the distortion in the direction of the body. This is the very origin of gravity we know.
References
1. Verlinde, E. On the Origin of Gravity and the Laws of Newton. J. High Energ. Phys. (2011) 2011: 29. https://doi.org/10.1007/JHEP04(2011)029.
2. Zee, A. Quantum Field Theory in a Nutshell (second ed.). Princeton University Press (2010), p. 172, 434–435. ISBN 978-0-691-14034-6.
3. Kobakhidze, A. Gravity is not an entropic force. Phys. Rev. D83, 021502 (2011).
4. Hamber, H.W. Quantum Gravitation – The Feynman Path Integral Approach. Springer Publishing (2009). ISBN 978-3-540-85292-6.
5. Treschman, K.J. Recent astronomical tests of general relativity. Int. J. Phys. Sci. 10, 90-105 (2015).
6. Einstein, A. Näherungsweise Integration der Feldgleichungen der Gravitation. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin, part 1: 688–696 (1916).
7. Einstein, A. Über Gravitationswellen. Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften Berlin, part 1: 154–167 (1918).
8. Castelvecchi, D., Witze, W. Einstein's gravitational waves found at last, Nature News (11 February 2016). doi:10.1038/nature.2016.19361. Retrieved 2016-02-11.
9. Abbott, B.P. et al. (LIGO Scientific Collaboration and Virgo Collaboration), Observation of Gravitational Waves from a Binary Black Hole Merger, Phys. Rev. Lett. 116, 061102 (2016).
10. https://opik.fyysika.ee/index.php/book/section/8642#/section/864211. Young, T. Bakerian Lecture: Experiments and calculations relative to physical optics. Phil. Trans. Royal Soc. 94, 1-16 (1804).12. Michelson, A.A., Morley, E.W. On the Relative Motion of the Earth and the Luminiferous Ether. Am. J. Sci. 34, 333-345 (1887).
13. Milonni, P.W. The Quantum Vacuum: An Introduction to Quantum Electrodynamics. Boston: Academic Press. 1994. ISBN 0124980805.
14. de la Pena, L., Cetto, A.M. The Quantum Dice: An Introduction to Stochastic Electrodynamics, Springer 1996. ISBN 978-94-015-8723-5.
15. Davies, P. The Goldilocks Enigma. First Mariner Books, p. 43 (2006). ISBN 978-0-618-59226-5.
16. Dirac, P.A.M.A. Theory of Electrons and Protons. Proc. R. Soc. Lond. 126, 360–365 (1930).
17. Anderson, C.D. The Positive Electron. Phys. Rev. 43, 491–494 (1933).
18. Krautkrämer, J., Krautkrämer, H. Ultrasonic testing of materials. 4th fully revised edition (1990), Springer-Verlag, Berlin, Germany, p. 497.
19. Kinsler, L.E., Frey, A.R., Coppens, A.B., Sanders, J.V. Fundamentals of acoustics. 4th Ed. (2000), John Wiley and sons Inc., New York, USA.
20. Queheillalt, D.T., Wadley, H.N.G. Temperature dependence of the elastic constants of solid and liquid Cd0.96Zn0.04Te obtained by laser ultrasound. J. Appl. Phys. 83, 4124-4133 (1998).
21. Vogt, C., Laihem, K., Wiebusch, C. Speed of sound in bubble-free ice. J. Acoust. Soc. Am. 124, 3613-3618 (2008).
22. Upadhyay, A.K., Sharma, B.S. Analysis of sound velocities and elastic moduli of some minerals. Indian J. Pure & Appl. Phys. 49, 30-34 (2011).
23. https://refractiveindex.info/
24. Emilio, M., Kuhn, J.R., Bush, R.I., Scholl, I.F. Measuring the Solar Radius from Space during the 2003 and 2006 Mercury Transits. Astrophys. J. 750, 135-142 (2012).12
25. de Broglie, L. The Reinterpretation of Wave Mechanics. Found. Phys. 1, 5-15 (1970).
26. McEvoy, J. P., Zarate, O. Introducing Quantum Theory. Totem Books (2004) p. 110–114. ISBN 978-1-84046-577-8.
27. Arndt, M., Nairz, O., Voss-Andreae, J., Keller, C., van der Zouw, G., Zeilinger, A. Wave-particle duality of C60. Nature 401, 680-682 (1999).
28. Davisson, C.J., Germer, L.H. Reflection of Electrons by a Crystal of Nickel. Proc. Natl. Acad. Sci. USA 14, 317-322 (1928).
29. Thomson, G.P. Diffraction of Cathode Rays by a Thin Film. Nature 119, 890 (1927).
30. Doak, R.B., Grisenti, R.E., Rehbein, S., Schmahl, G., Toennies, J.P., Wöll, Ch. Towards Realization of an Atomic de Broglie Microscope: Helium Atom Focusing Using Fresnel Zone Plates. Phys. Rev. Lett. 83, 4229–4232 (1999).
31. Beiser, A.Concept of Modern Physics. 6th Ed. McGraw Hill. p. 95. ISBN 0–07–244848–2.
32. Resnick, R., Eisberg, R. Quantum Physics of Atoms, Molecules, Solids, Nuclei and Particles (2nd ed.). New York: John Wiley & Sons (1985). ISBN 978-0-471-87373-0.
33. Rosen, J., Gothard, L.Q. Encyclopedia of Physical Science. Infobase Publishing (2009) p. 155. ISBN 978-0-8160-7011-4.13
Appendix [A1]
Deflection of light in the distorted solid vacuum
Einstein predicted using the GR theory that light deflects while passing by the Sun, as exaggeratedly illustrated in Figure 1. The light deflection by the Sun was demonstrated in the observation of Eddington's total solar eclipse on May 29, 1919.1 Here we calculate the deflection angle based on our new vacuum paradigm. When light from a distance travels toward the Sun, the movement in an infinitesimal time interval of dt can be divided into the movement dr toward the solar center and that dq in the circumferential direction of the Sun while advancing by cdt = dp, as shown in Figure 2. Due to the presence of the Sun, the solid vacuum is distorted. The length in the radial direction to the solar center is shortened by rS to give the distortion rS/r at r according to Eq. (11) of the main text. A light wave moves in the radial direction faster than in the circumferential direction. If there is no distortion of the solid vacuum, then dq should be equal to dq + ds, namely ds = 0, where ds is the retarded path (compared to the path in the radial direction) of light due to the distortion during dt. ds is given as
𝑑𝑠2=𝑑𝑞2×(𝑟𝑆/𝑟)2=(𝑑𝑝2−𝑑𝑟2)(𝑟𝑆/𝑟)2 (1).
The distance r away from the solar center is related to the distance p away from the tangential Solar Surface as
𝑟2=𝑝2+𝑅2 → 𝑝𝑑𝑝=𝑟𝑑𝑟 (2).
Here R is the radius of the Sun. From Equation (2), Equation (1) is rearranged to
𝑑𝑠2=𝑑𝑝2[(𝑟2−𝑝2)/𝑟2](𝑟𝑆/𝑟)2=𝑑𝑝2(𝑅2/𝑟2)(𝑟𝑆/𝑟)2 ,
so that
𝑑𝑠=(𝑟𝑆𝑅/𝑟2)𝑑𝑝=𝑟𝑆𝑅/(𝑝2+𝑅2)𝑑𝑝 (3).

Figure 1. Deflection of light by the Sun. The deflection angle is highly exaggerated for the presentation.
Integrating Equation (3) from -∞ to 0 and from the equivalence,
∫[1/(𝑥2+𝑎2)]𝑑𝑥=(1/𝑎)tan−1(𝑥/𝑎) (4),
we have the light deflection in length at the tangential Solar Surface as
s=∫0-∞[𝑟𝑆𝑅/(𝑝2+𝑅2)]𝑑𝑝=𝑟𝑆[tan−1(0/𝑅)−tan−1(−∞/𝑅)]=π𝑟𝑆/2 (5).
The deflection angle φ = ds/dp in radian at the tangential Solar Surface is given for p = 0 or r = R in Equation (3), as
φ =𝑑𝑠/𝑑𝑝=𝑟𝑆/𝑅 (6).
This deflection angle becomes twice for the Earth observer since the light has the same effect as it reaches the Earth observer. The total deflection Φ will then be
Φ =2φ=4𝐺𝑀/(𝑐2𝑅) (7)
This equation is the same as that derived from Einstein's GR theory.2
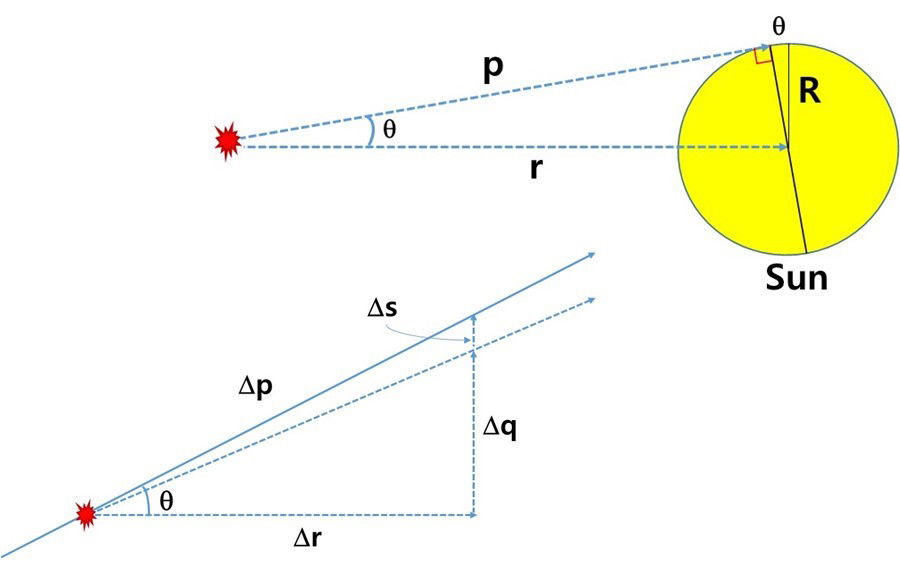
Figure 2. Division of the light path toward the Sun: r, radial direction; q, circumferential direction.
We consider, however, that the path of deflected light is asymmetric in terms of the elapsed length of light. The maximum deflection of light from the light source at the Solar Surface is given as Equation (5) by integrating Equation (4) from –∞ to 0. Meanwhile, the deflection from the Solar Surface to the Earth’s observer is calculated by integrating Equation (4) from 0 to 215 R (R is the solar radius, 695,700 km.3 The distance from Earth to the Sun is 149,597,870 km.4). The deflection S is then
s=∫0215𝑅[𝑟𝑆𝑅/(𝑝2+𝑅2)]𝑑𝑝=𝑟𝑆[tan−1(215𝑅/𝑅)−tan−1(0/𝑅)] (8).
The light deflection from the Solar surface to Earth is around 0.4% less than that of Equation (5). So the total deflection angle in radian should be modified to
Φ =2𝐺𝑀/(𝑐2𝑅) + 1.992𝐺𝑀/(𝑐2𝑅)=3.992𝐺𝑀/(𝑐2𝑅) (9).
The first term in the middle of Equation (9) is the light deflection from the light source to the Solar Surface and the second term is the light deflection from the Solar Surface to Earth.
References of [A1]
1. Dyson, F.W., Eddington, A.S., Davidson, C.R. A Determination of the Deflection of Light by the Sun's Gravitational Field, from Observations Made at the Solar eclipse of May 29, 1919. Phil. Trans. Roy. Soc. A. 220, 291-333 (1920).
2. Treschman, K.J. Recent astronomical tests of general relativity. Int. J. Phys. Sci. 10, 90-105 (2015).
3. Mamajek, E.E., Prsa, A., Torres, G., et, al. (2015), "IAU 2015 Resolution B3 on Recommended Nominal Conversion Constants for Selected Solar and Planetary Properties", arXiv:1510.07674 [astro-ph.SR].
4. Pitjeva, E. V., Standish, E. M. (2009). "Proposals for the masses of the three largest asteroids, the Moon–Earth mass ratio and the Astronomical Unit". Celestial Mechanics and Dynamical Astronomy. 103 (4): 365–372. doi:10.1007/s10569-009-9203-8.
Appendix [A2]
Precession of the perihelion of Mercury
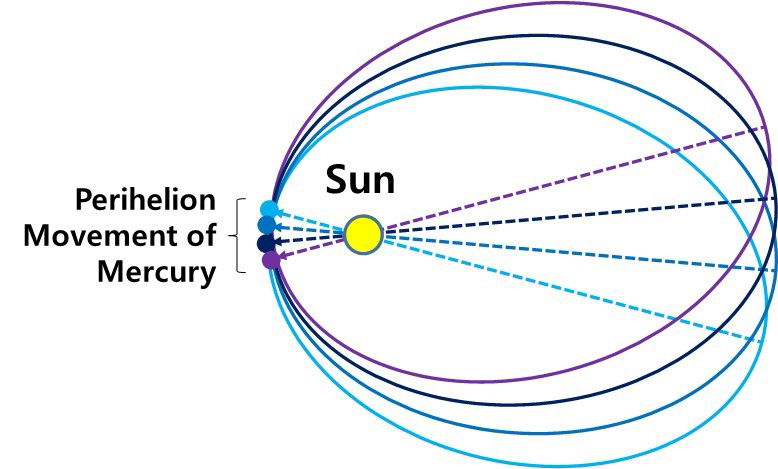
Figure 1. Schematic and exaggerated precession of the perihelion of Mercury.
In the solar system, the perihelion of the planet to the Sun is not fixed but rotates for various reasons.1 This rotation is called the perihelion precession, and the main cause is the gravitational influence of the other planets. The orbit of Mercury deviates from the center of the Sun to be an elliptical one, and the perihelion of Mercury rotates 574.1"(arcseconds) per 100 years, as shown in Figure 1. The estimate of the precession based on Newtonian dynamics is 532.3", about 42" different from the observed value.2 In the GR theory, the rotation of the elliptical orbital axis of Mercury is explained in terms of the change in the spacetime curvature due to gravity. Einstein used the GR theory to calculate the precession ε in radian for the elliptic orbit of the planet, as 3
𝜺=𝟐𝟒𝝅𝟑𝒓𝒂𝟐/[𝑻𝟐𝒄𝟐(𝟏−𝒆𝟐)] (1).
Here ra is the semi-major axis, e the eccentricity and T the orbital period, respectively. For Mercury, ra is 5.79 × 1010 m, e = 0.206 and T = 87.97 days. The precession for one revolution is then calculated to be 5.028×10-7 radians, corresponding to about 43.2" per 100 years, since Mercury is revolving about 415 times for 100 years. Other planets are less dominant than Mercury regarding the precession, though they do such a perihelion precession: 3.84" and 8.62" per 100 years for Earth and Venus, respectively.4 A recently-discovered double pulsar system, PSR 1913+16, has a value of 4.2° per year, which is also well explained by the GR theory.5 On the other hand, the Relativistic Newtonian Dynamics (RND) model, a simple modification of the Newtonian dynamics, is also well explaining the precession of the perihelion of Mercury 6,7 and that of the binary system PSR J0737-3039A/B 8 without relying on curving spacetime in the GR theory. The RND model deals with the precession only by the relativistic velocity in the inertial frame of reference, so that it is similar to our approach to gravity from the inertial motion of a particle in terms of the distortion of the solid vacuum. However, like the GR relativity, this RND model did not pay any attention to the origin of gravity.According to our new vacuum paradigm, kinetic and gravitational potential energy are substantially the same distortion energy stored in the solid vacuum. In this context, it is simple and clear to understand the perihelion movement of the binary system like the Sun and Mercury in terms of the distortion of the solid vacuum. When Mercury makes one revolution around the Sun, the associated distortion is the radial one of rS and the circumferential one of ½rS, as evident from Eq. (11) and (12) of the main text. The total distortion involved is 1½rS, which is 3𝜋rS in terms of the orbital length. The vacuum is additionally distorted by 3𝜋rS from the track length 2𝜋rm, where rm is the mean radius of the orbit of Mercury around the Sun. Hence, the precession of Mercury expressed in Radian should be
𝜺=𝟑𝝅𝒓𝑺/𝒓𝒎 (2).
However, as there are several mean values for the orbital movement of Mercury: three means based on the aphelion and perihelion, and three means based on the elliptical movement of Mercury, as listed in Table 1 and 2, it is hard to determine the right radius for rm. Equation (2) is actually the same as Equation (1) if 𝒓𝒎=𝟐𝒓𝑨𝒓𝑷/(𝒓𝑨+𝒓𝑷), which is the harmonic means rh of rA and rP, the aphelion and perihelion of Mercury, respectively. Inserting the relation of Kepler’s third law, 𝑻𝟐/𝒓𝒂𝟑=𝟒𝝅𝟐/[𝑮(𝑴+𝒎)] to Equation (1) with the definition of eccentricity, 𝒆=(𝒓𝑨-𝒓𝑷)/(𝒓𝑨+𝒓𝑷), we have
𝜺=𝟔𝝅𝑮(𝑴+𝒎)/[𝒓𝒂𝒄𝟐(𝟏−𝒆𝟐)]=𝟑𝝅𝒓𝑺/[𝒓𝒂(𝟏−𝒆𝟐)]=𝟑𝝅𝒓𝑺/𝒓𝒉 (3).
When we apply the harmonic mean of the aphelion and perihelion, which is the calculation by GR, we have still a difference of 1.21" in the precession between the sum of the prediction and the observed, as shown in Table 3.
As Mercury is in the distortional field of the Sun, its rotation around the Sun will add additional distortion in this field, acting as a dragging force, which in turn causes the rotation of the axis connecting the center of Mercury and the Sun. The movement of Mercury can be divided into a pure rotational one and a radial one with the Sun as the reference point. For this reason, we may think the radius for the calculation of the precession should be different for each type of movement. Thus the precession expressed as Equation (2) may be modified to
𝜀=2𝜋𝑟𝑆/𝑟1+𝜋𝑟𝑆/𝑟2 (4).
The first term on the right-hand side of Equation (4) is due to the radial movement and the second term is due to the rotational movement of Mercury, respectively. What shall be the appropriate radius for r1 and r2 in Equation (4)? We have the least difference between the estimated and observed if we apply the harmonic mean of the elliptical orbit of Mercury to r1 and the geometrical mean of the aphelion and perihelion to r2. The difference is given in Table 3 as 0.0067". The reason for this coincidence is not clear for now and needs to be studied.The accumulated distortion in the solid vacuum by one rotation will be freed through the precession of the perihelion. One rotation plus the perihelion advance in the distorted solid vacuum means one rotation in the solid vacuum free of additional distortion. This is one of our interpretations of the movement of Mercury's perihelion in the regime of the new paradigm of vacuum.
Table 1. Radii based on the aphelion and perihelion of Mercury.
Radius | km | formula |
Aphelion Perihelion | 69,816,900 46,001,200 | rA rP |
Arithmetic mean Geometric mean Harmonic mean | 57,909,050 56,671,520 55,460,436 | (𝑟𝐴+𝑟𝑃)/2 √(𝑟𝐴𝑟𝑃) 2𝑟𝐴𝑟𝑃/(𝑟𝐴+𝑟𝑃) |
Table 2. Radii based on the elliptical orbit of Mercury.
Radius | km | formula |
Semi-major axis Semi-minor axis | 57,909,050 56,671,523 | 𝑟𝑎 𝑟𝑏 |
Arithmetic mean Geometric mean Harmonic mean | 57,290,287 57,286,945 57,283,6042 | (𝑟𝑎+𝑟𝑏)/2 √(𝑟𝑎𝑟𝑏) 2𝑟𝑎𝑟𝑏/(𝑟𝑎+𝑟𝑏) |
Table 3. Estimated precession of Mercury by the cause of the precession.
| Cause of the precession | Estimated precession (arc seconds/100yr) | Comments | |
| Gravitational effect of other planets | 532.3035 | The harmonic mean of the perihelion and aphelion | |
| Distortion of space-time due to GR theory | 42.9799 | ||
| Distortion of the solid vacuum | 41.7632 | The geometric mean of the perihelion and aphelion and the harmonic mean of the elliptical orbit | |
| Other minor effects | 0.0266 | ||
| Sum of the prediction | 575.31 | 574.0933 | |
| Observed value | 574.10±0.65 | ||
| Difference in the precession | 1.21 | 0.0067 | |
References of [A2]
1. Park, R.S., Folkner, W.M., Konopliv, A.S., Williams, J.G., Smith, D.E., Zuber, M.T. Precession of Mercury’s Perihelion from Ranging to the MESSENGER Spacecraft. Astronomical J. 153, 121-127 (2017).
2. Le Verrier, U. Lettre de M. Le Verrier á M. Faye sur la théorie de Mercure et sur le mouvement du périhélie de cette planète. Comptes rendus hebdomadaires des séances de l'Acadèmie des sciences (Paris) 49, 379-383 (1859).
3. Hawking, S. On the Shoulders of Giants. The Great Works of Physics and Astronomy. Philadelphia, Pennsylvania, USA: Running Press. p. 1243, Foundation of the General Relativity. ISBN 0-7624-1348-4.
4. Biswas, A., Mani, K.R.S. Relativistic perihelion precession of orbits of Venus and the Earth. Cen. Euro. J. Phys. 6, 754-758 (2008).
5. Weisberg, J.M., Taylor, J.H. The Relativistic Binary Pulsar B1913+16: Thirty Years of Observations and Analysis. Binary Radio Pulsars, Ed. F.A. Rasio and I.H. Stairs. ASP Conference Series. 328. Aspen, Colorado, USA: Astronomical Society of the Pacific (2005).
6. Friedman, Y. Relativistic Newtonian Dynamics under a central force. Eur. Phys. Lett. 116, 19001 (2016).
7. Friedman, Y., Steiner, J.M. Predicting Mercury’s Precession using Simple Relativistic Newtonian Dynamics, Eur. Phys. Lett. 113, 39001 (2016).
8. Friedman, Y., Livshitz, S., Steiner, J.M. Predicting the relativistic periastron advance of a binary without curving spacetime. V2. Eur. Phys. Lett. 116, 59001 (2016).